전체 컨셉
How can we identify causal effects when we are in the presence of unobserved confounding?
-> One popular way is to find and use "Instrumental variables".
1. What is an Instrument?
변수 Z가 instrument로 간주되기 위해서는 세 개의 Assumption을 만족해야 한다.
Assumption 1. (Relevance) Z has a causal effect on T
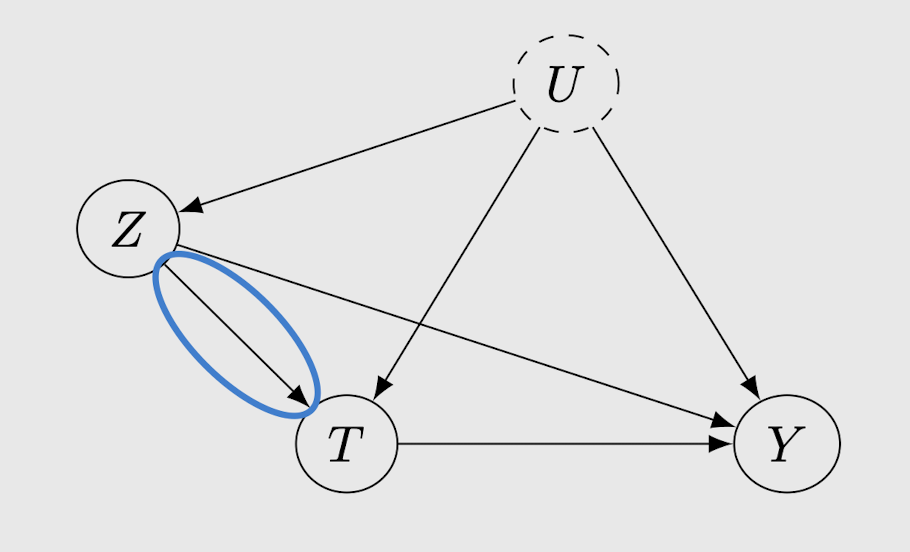
Assumption 2. (Exclusion Restriction) Z causal effect on Y is fully mediated by T
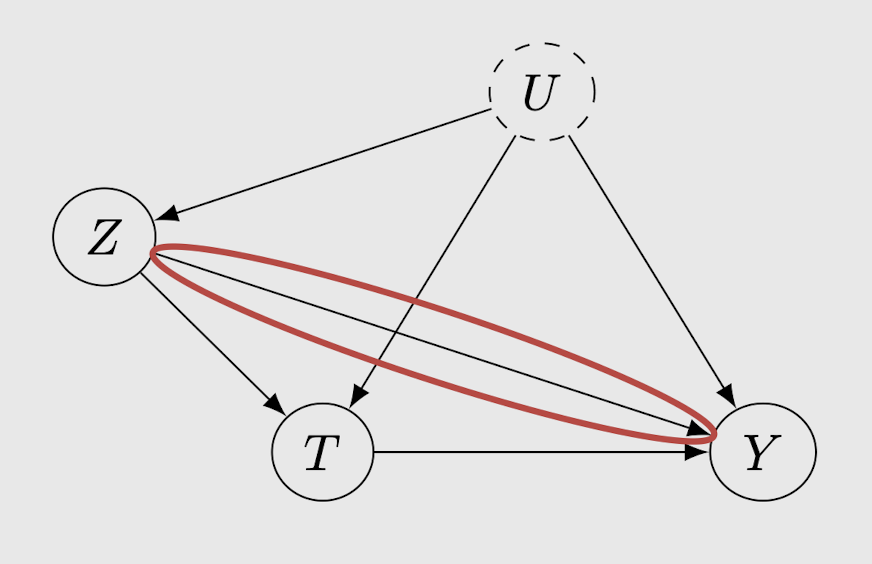
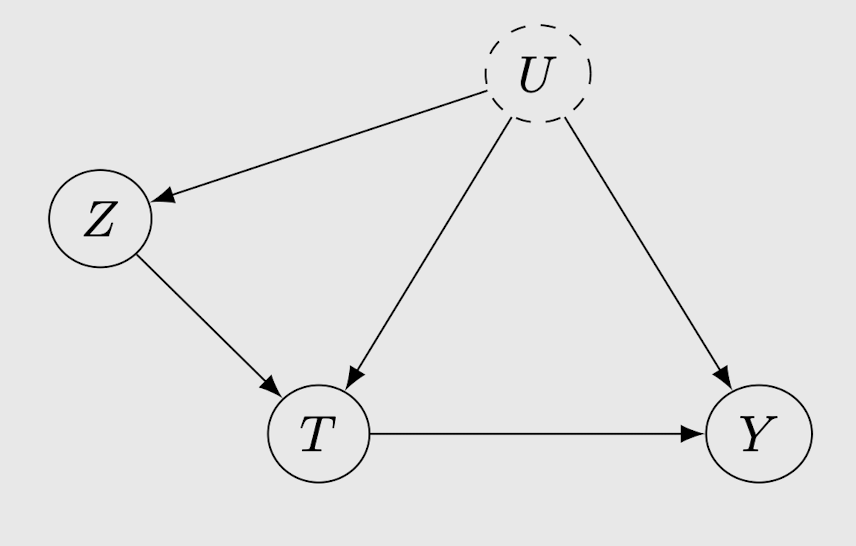
1. Y를 나타내는 구조 방정식 상에서 Z를 배제
2. T를 거치지 않고 Z와 Y 간의 causal association을 만드는 모든 구조 방정식을 배제
=> causal graph 상에서 변수 간의 edges 배제했기 때문에, Z에서 Y로 가는 모든 causal paths는 T를 지난다.
We assume that the causal effect of Z on Y is unconfounded
Assumption 3. (Instrumental Unconfoundedness) There are no backdoor paths from Z to Y

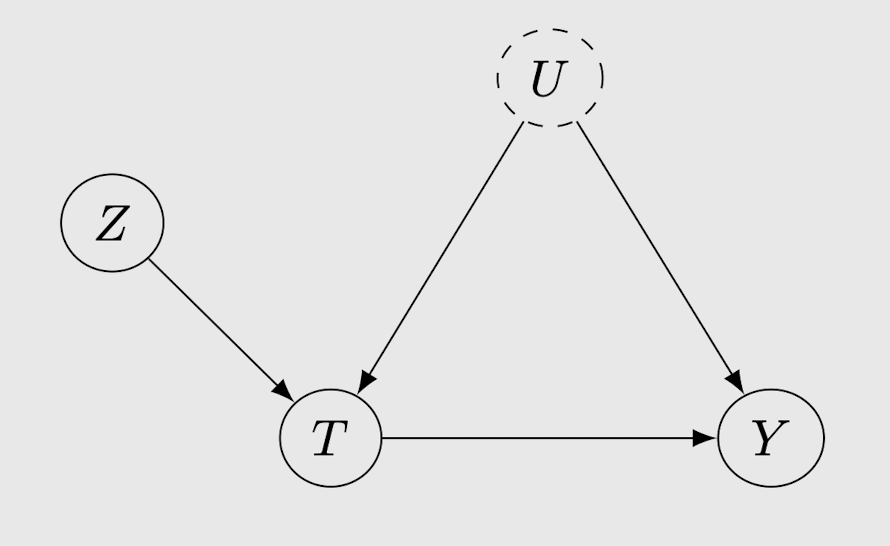
backdoor path가 있다면 제거
=> Z는 이제 완전히 Unconfounded!
Conditional Instruments
observed variable(W)에 대해서 조건부 unconfoundedness가 있더라도 intrumental variables는 여전히 잘 동작
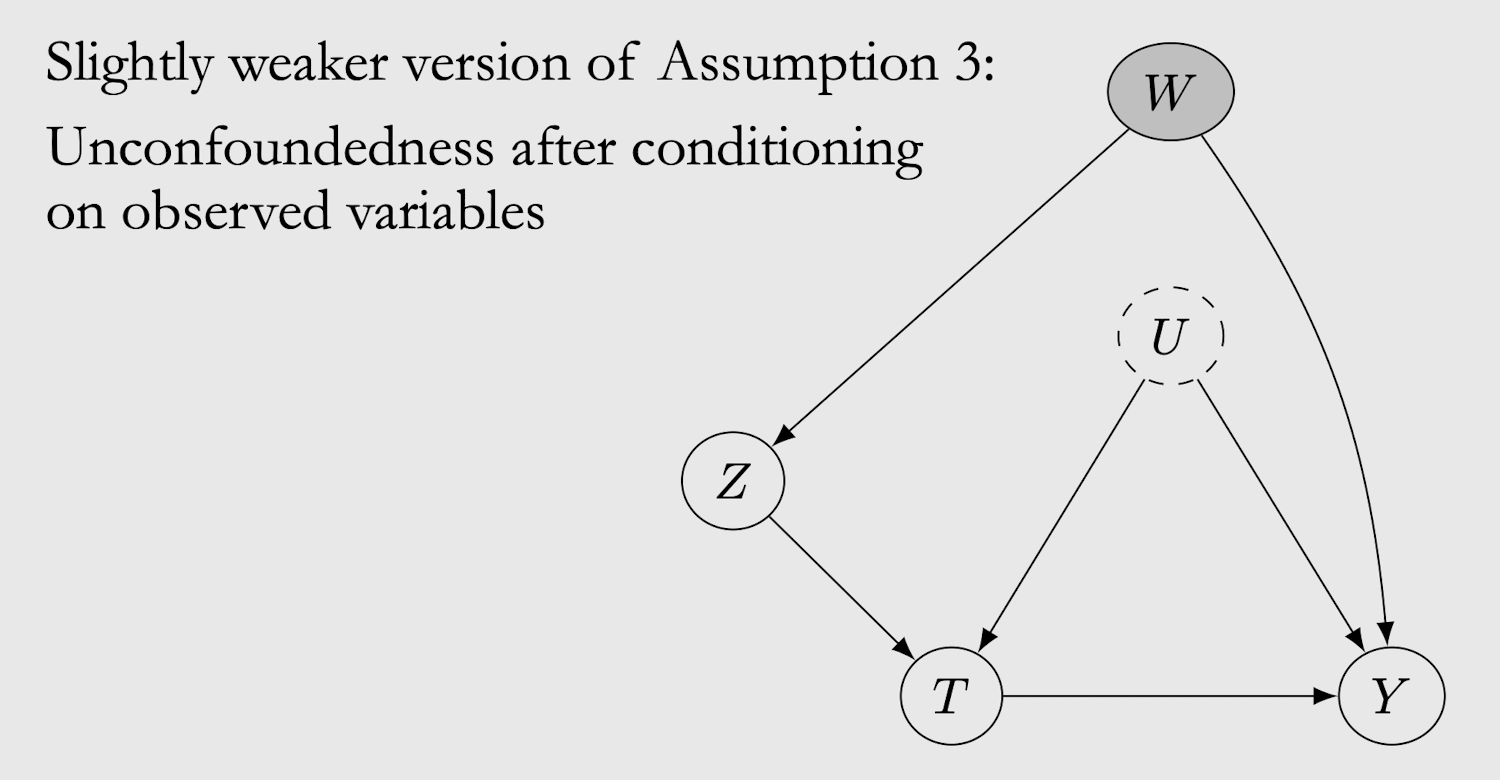
2. No Nonparametric Identification of the ATE
2.1. Q&A
Question?

Answer?
- Assumption을 만들 필요가 없을 때 Nonparametric Identification을 가질 수 있음
- 하지만, Instrumental Variables는 위와 같은 3가지 Assumption이 존재하기 때문에 causal effect를 nonparametrically 식별할 수 없음
또한,
Nonparametric Identification을 만족하는 조건은 아래와 같음
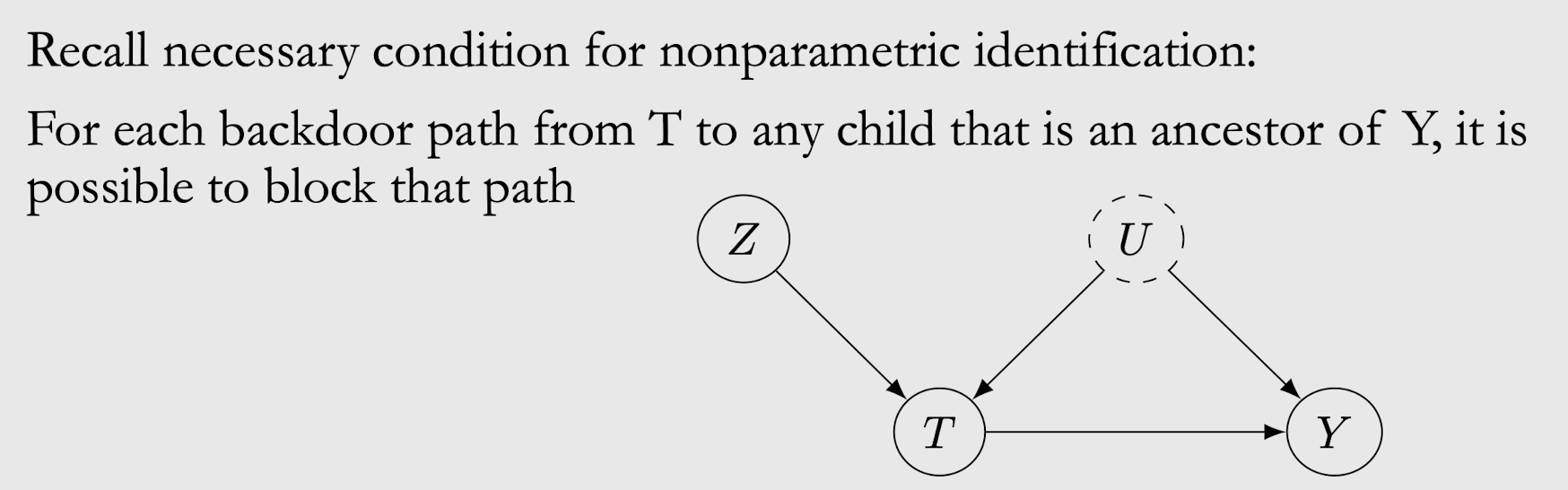
1. Y는 자기 자신의 ancestor
2. Y는 T의 child
3. U는 unobserved confounder이기 때문에 backdoor path를 block 불가능(ch6 backdoor path block 조건 찾아보기!)
=> T에서 Y로 가는 backdoor path인 U를 block할 수 없기 때문에 Nonparametric Identification 조건을 만족하지 않음
3. Warm-Up: Binary Linear Setting
Assumption 4. (Linear Outcome)

Setting.
- T and Z are binary
Z가 방정식에 표현되지 않은 이유는 'Assumption 2' 때문
Assumption 2. (Exclusion Restriction) Z causal effect on Y is fully mediated by T
-> T를 거치지 않고 Z와 Y 간의 causal association을 만드는 모든 구조 방정식을 배제


Z-Y 관계에 대한 associational difference는 아래 식으로 나타낼 수 있음

Wald Estimand
아래 식에서 분모는 relevance assumption 때문에 0이 아님 -> 우항이 undefined 될 일 없음
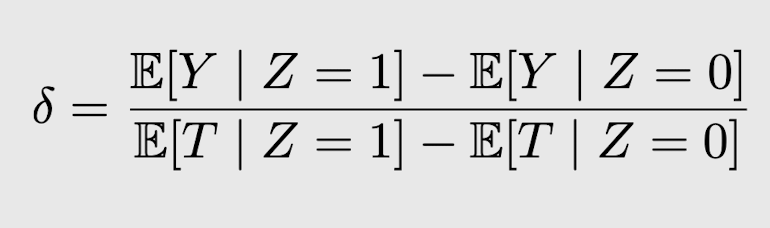
instrument Z -> Y로 가는 backdoor path가 없기 때문에,
Z -> Y path의 effect를 하나씩 살펴볼 수 있음
또한,
Z -> T / T -> Y 와 같이 causal effect가 있는 directed path를 각 coefficient의 곱으로 생각해볼 수 있음
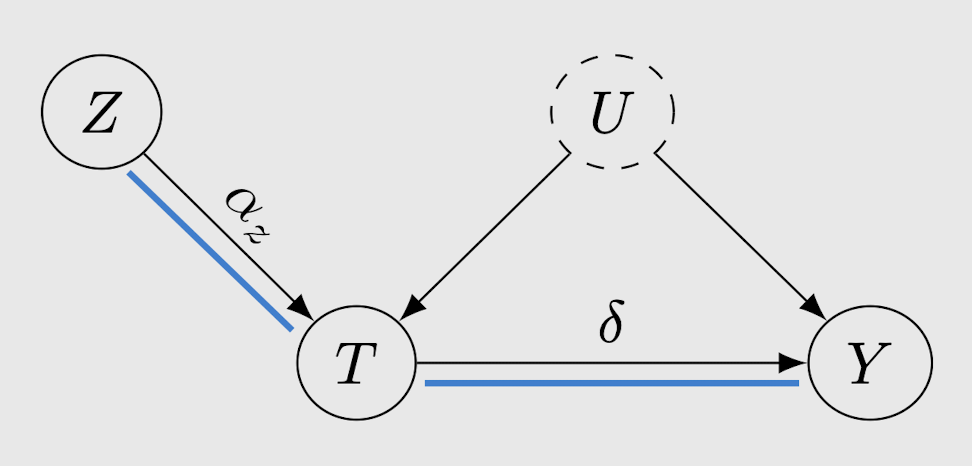
Preposition 9.1 식에 대입해보면 아래와 같은 식으로 변경할 수 있음
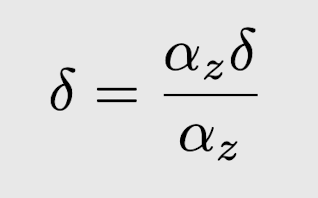

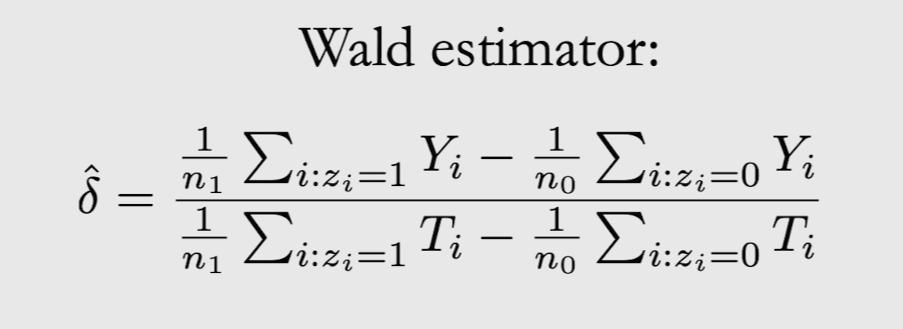
4. Continuous Linear Setting
Setting.
- T and Z are continuous
- Assumption 4

아래 식에서 분모는 relevance assumption 때문에 0이 아님 -> 우항이 undefined 될 일 없음

Two-stage least squares estimator
Wald Estimator와 유사한 natural estimator
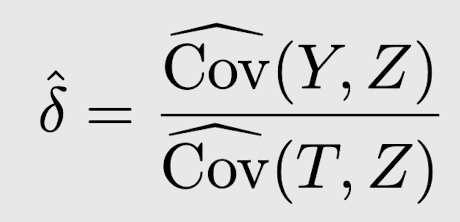

- T^는 U의 함수가 아니므로, 해당 edge 제거
- T^에서 Y로 가는 backdoor path 없음
- 현재의 association이 causation
+ binary setting에서도 적용 가능
5. Nonparametric Identification of Local ATE
Assumption 만들지 않고도 indentification을 위한 instrumental variables를 만들 수 있음
1. settle for a more specific causal estimand than the ATE
2. swap the linearity assumption out for a new assumption
Potential Outcomes Notation with Instruments
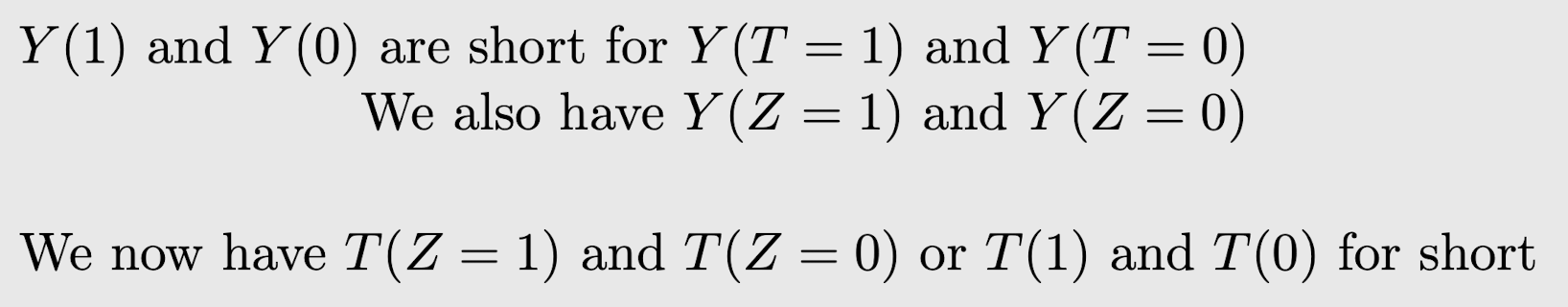
Principal Strata

- Always/Never-takers: Y에 대한 Z의 causal effect는 0
Monotonicity Assumption
: LATE(Local ATE) Identification에 필요

- instrument value가 1인 treatment의 값이 크거나 같아야함
Deriving Local ATE Identification
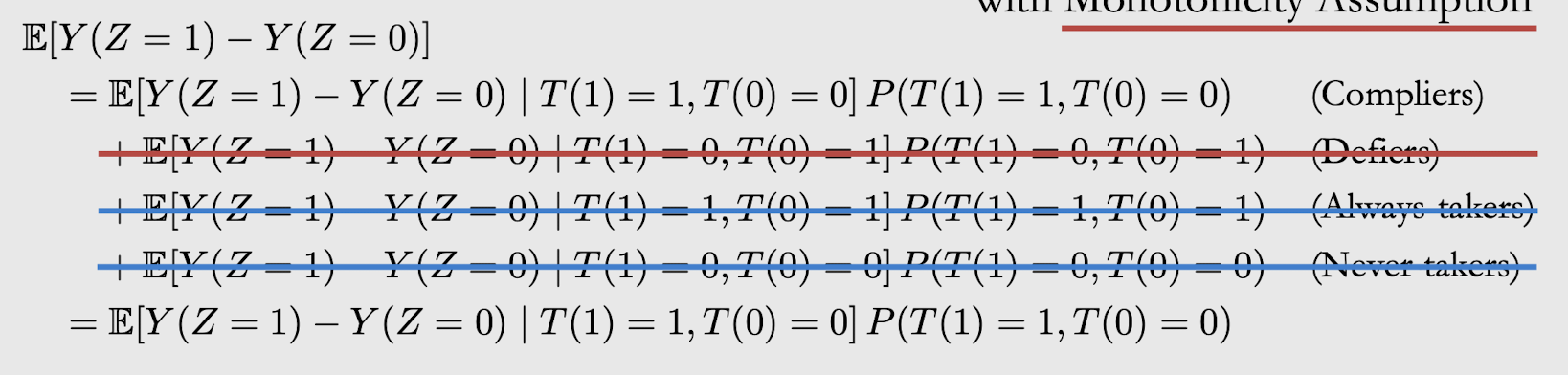
- Monotonicity Assumption을 하기 때문에 Defiers 제거
- Always/Never-takers: Y에 대한 Z의 causal effect는 0
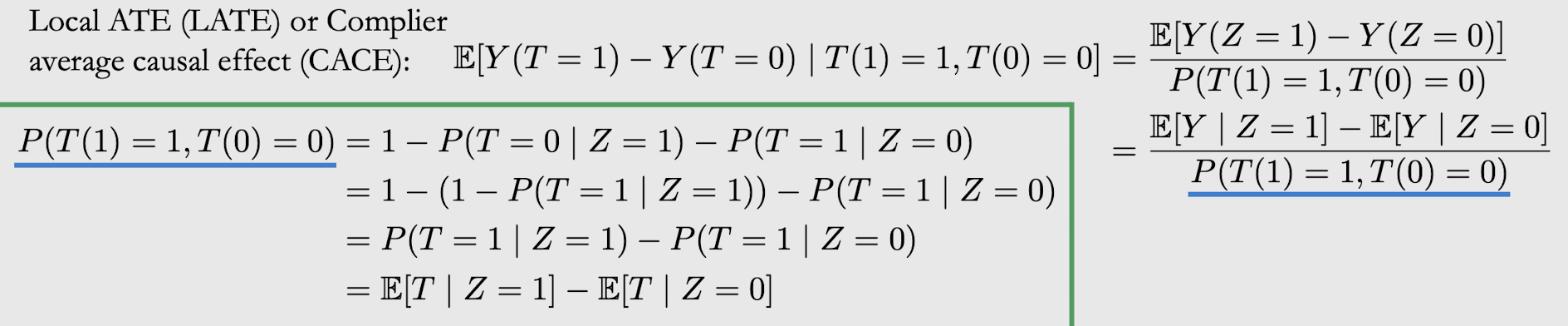

- LATE는 subpopulation, ATE는 whole population (그래서 아래와 같은 문제 생김)

6. More General Settings for ATE Identification
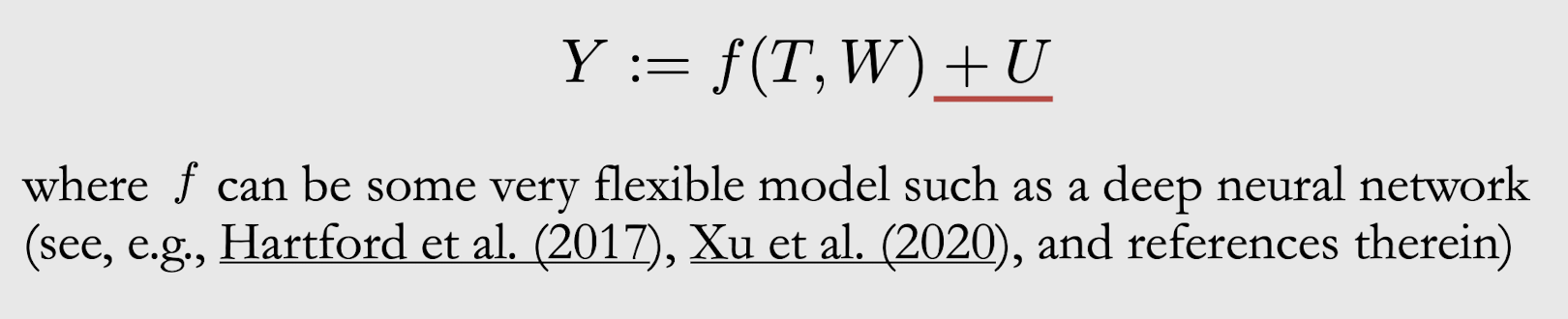
- 딥 러닝으로 f를 모델링

- point보다는 set을 identification하는 것이 부가적인 노이즈 assumption을 완화시킴
- 그래서, U를 방정식에서 제거
'AI > 공부' 카테고리의 다른 글
| [Book] 한국어 임베딩 (0) | 2019.11.09 |
|---|---|
| CNN (0) | 2019.09.30 |
| RNN & Automata (오토마타) (0) | 2019.09.24 |



댓글